第一章：为什么位置编码如此重要？

在人工智能浪潮席卷全球的今天，大型语言模型（LLM）无疑是那朵最璀璨的浪花。从能够对答如流、撰写代码的ChatGPT，到在各个领域展现出惊人创造力的Llama、Qwen、ChatGLM等模型，我们正亲眼见证一个由算法和数据驱动的智能新纪元的到来。

这些模型似乎拥有了以往只属于人类的特权——深刻理解并灵活运用语言。它们魔法般能力的基石，几乎无一例外地指向了同一个革命性的架构——Transformer。然而，正是这个开启了新时代的强大架构，却隐藏着一个与我们直觉相悖的、根本性的“缺陷”：它天生无法感知顺序。

1.1 Transformer的“顺序盲”：一个美丽的“缺陷”

要理解这个“缺陷”，我们必须深入Transformer的心脏——自注意力（Self-Attention）机制。

这是一种极其强大的设计，它彻底摆脱了传统RNN（循环神经网络）和LSTM（长短期记忆网络）那种逐词处理、顺序依赖的束缚。自注意力机制允许模型在处理序列中的任意一个词（Token）时，都能够瞬间“看到”并评估与序列中所有其他词的关联性。

想象一下，你在阅读一个长句，自注意力机制就像赋予了你一种超能力，让你的目光可以同时聚焦在句子的每一个词上，并瞬间构建出一张复杂的关系网络：哪个词是主语，哪个动词作用于它，哪个形容词修饰了它。

正是这种全局的、并行的视野，赋予了Transformer无与伦比的捕捉长距离依赖关系的能力，这在处理复杂语言现象时至关重要。

然而，这种能力的代价是什么？是秩序的消解。在自注意力机制的数学实现中，其核心是 Query、Key、Value三个向量的矩阵运算。模型通过计算一个词的 Query向量与其他所有词的 Key向量的点积，来得到注意力分数。这个过程本质上就像是将句子中的所有词丢进一个“袋子”里，然后两两之间进行比较，找出关联性。

对于这个“袋子”而言，“猫咬狗”和“狗咬猫”在初始看来并无本质区别，因为它们都含有“猫”、“狗”、“咬”这三个元素。自注意力机制的计算是 置换不变（Permutation Invariant） 的，即打乱输入序列的顺序，得到的注意力分数矩阵（在不考虑位置编码的情况下）除了行和列的顺序变化外，其内部的值是相同的。

这种对顺序的“漠视”，我们称之为“顺序盲”。这不仅仅是理论上的小问题，在实际应用中是致命的。语言的精髓恰恰在于其顺序性：

语义：“我借给你一本书”与“你借给我一本书”，意义截然相反。
语法：主谓宾的结构定义了谁是动作的发出者和承受者。
逻辑：在代码中，x = a + b; y = x * c; 与 y = x * c; x = a + b; 的结果天差地别。

因此，为了让Transformer架构能够真正理解并处理语言，研究者们必须找到一种方法，将序列中每个词的绝对或相对位置信息“注入”到模型中。这项至关重要的技术，就是位置编码（Positional Encoding）。

1.2 传统位置编码的探索与困境

在RoPE（旋转位置编码）革命性地改变游戏规则之前，业界为了解决Transformer的“顺序盲”问题，已经进行了漫长而富有成效的探索。这些探索主要沿着两条截然不同的技术路径展开：

一条是简单直接、依赖模型学习能力的可学习绝对位置编码；
另一条则是充满数学巧思、试图从根本上定义位置关系的正弦位置编码。

然而，尽管它们在各自的时代都取得了巨大的成功，但最终都遇到了难以逾越的瓶颈，而正是这些瓶颈，催生了对更优解决方案的迫切需求。

1.2.1 可学习绝对位置编码：简单粗暴，但有“天花板”

最符合深度学习“万物皆可学习”范式的方案，便是将位置信息也视为一种可学习的参数。这种方法的思路极其直观：

创建位置查找表：我们为模型可能遇到的每一个绝对位置（第0位，第1位，第2位，…，直到预设的最大长度N）都创建一个专属的、维度与词向量相同的向量。这些向量在训练开始时随机初始化。
向量相加：在将一个词送入Transformer模型之前，我们先获取它的词义嵌入向量（Token Embedding），然后根据它在序列中的绝对位置，从上述查找表中取出对应位置的向量（Position Embedding）。最后，将这两个向量逐元素相加，形成最终的输入表示。

\text{InputEmbedding} = \text{TokenEmbedding}_{\text{word}}+\text{PositionEmbedding}_{\text{pos}}

端到端学习：这些位置向量将作为模型参数的一部分，在训练过程中通过反向传播不断被优化，模型会自主地学习到如何利用这些向量来理解位置信息。

这种方法简单直接，易于实现，并在以BERT为代表的一系列早期预训练模型中被证明非常有效。模型确实能够从海量数据中学会这些位置向量所蕴含的意义。

然而，它的“阿喀琉斯之踵”也同样致命，那就是外推性（Extrapolation）几乎为零。

“外推”指的是模型处理比训练时所见过的、更长的序列的能力。可学习位置编码的本质，就是一个巨大且固定的查找表（Lookup Table）。

想象一下，如果我们设定模型的最大训练长度为512（max_position_embeddings=512），那么这个查找表中就只有512个从0到511的位置向量。在漫长的训练过程中，模型反复见到并优化了这512个向量。

现在，当模型训练完成，进入推理阶段时，如果用户输入了一个长度为513的句子，灾难就发生了。当模型处理到第513个词时（位置索引为512），它需要去查找表里获取该位置的编码。但查找表中根本没有这个位置的条目！

程序通常会返回一个未经训练的、随机初始化的向量。这个向量对于已经高度优化的模型来说，无异于一个刺耳的噪声信号。它会严重干扰后续的注意力计算，导致模型输出的结果毫无逻辑，性能出现断崖式的下跌。

这个由最大训练长度所决定的、无法被突破的“长度天花板”，成为了可学习位置编码方案的根本局限。

它使得模型难以被应用于需要处理长文档摘要、长篇小说分析、多轮长对话等日益增多的现实场景中，促使研究者们去寻找不依赖学习、具备理论外推能力的新方法。

1.2.2 正弦位置编码：优雅的设计，破碎的理想

为了从根本上解决外推性问题，原版Transformer论文《Attention Is All You Need》的作者们提出了一种极具数学美感的方案——正弦位置编码（Sinusoidal Position Encoding）。它彻底抛弃了学习的方式，转而用一组固定的、确定性的公式来生成位置编码，其设计中蕴含着深刻的数学巧思。

设计的核心理念

正弦编码的核心目标是创造一种编码方式，同时满足以下几个关键特性：

唯一性：为每个时间步（位置）输出一个独一无二的编码。
确定性：对于相同长度的序列，不同模型间的位置编码应该是相同的，不依赖于训练过程。
外推性：能够轻松地泛化到比训练时更长的序列长度。
蕴含相对信息：编码本身的设计应该能让模型更容易地捕捉到相对位置关系。

公式的精妙构造

为了实现这些目标，作者们设计了如下公式。对于一个位于 pos位置的 d维向量，其位置编码的第 i个维度的值由以下公式确定：

\begin{aligned} PE_{(pos, 2i)} &= \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) \\ PE_{(pos, 2i+1)} &= \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) \end{aligned}

这里的变量含义如下：

pos：代表词元在序列中的绝对位置，从0开始。
i：代表编码向量中的维度索引，从0到 d_{\text{model}}/2 - 1。
d_{\text{model}}：代表模型的隐藏层维度，即词向量和位置编码向量的维度。

这个公式的精髓在于它巧妙地将不同频率的正弦波和余弦波组合在了一起。分母中的 10000^{2i/d_{\text{model}}} 是一个波长项。当维度索引 i很小时，分母接近1，波长很短，频率很高。随着 i的增大，分母越来越大，波长也随之指数级增长，频率则降低。

这意味着，位置编码的低维部分（i较小）对应高频信号，它们在相邻位置间变化得非常快；而高维部分（i较大）对应低频信号，它们的变化非常平缓，可以用来编码更宏观的位置信息。这种多尺度、多频率的设计，就像用不同周期的时钟（秒针、分针、时针）来记录时间一样，共同为每一个位置 pos生成了一个独一无二的“时间戳”向量。

理想中的相对位置关系

正弦编码设计的最高明之处，在于它理论上具备了表达相对位置的能力。这源于三角函数的一个基本性质：和差角公式。

考虑任意一个相对偏移量 k，我们想知道位置 pos+k的编码与位置 pos的编码之间有什么关系。让我们关注任意一个维度对

(PE_{(pos, 2i)}, PE_{(pos, 2i+1)})

令

\omega_i = 1/10000^{2i/d_{\text{model}}}

则有：

\begin{aligned} PE_{(pos+k, 2i)} &= \sin((pos+k)\omega_i) = \sin(pos\omega_i)\cos(k\omega_i) + \cos(pos\omega_i)\sin(k\omega_i) \\ PE_{(pos+k, 2i+1)} &= \cos((pos+k)\ omega_i) = \cos(pos\omega_i)\cos(k\omega_i) - \sin(pos\omega_i)\sin(k\omega_i) \end{aligned}

这个关系可以用矩阵形式优美地表达：

\begin{pmatrix} PE_{(pos+k, 2i)} \\ PE_{(pos+k, 2i+1)} \end{pmatrix} = \begin{pmatrix} \cos(k\omega_i) & \sin(k\omega_i) \\ -\sin(k\omega_i) & \cos(k\omega_i) \end{pmatrix} \begin{pmatrix} PE_{(pos, 2i)} \\ PE_{(pos, 2i+1)} \end{pmatrix}

这个公式揭示了一个惊人的事实：位置 pos+k 的位置编码，可以通过对位置 pos 的编码进行一次线性变换（乘以一个旋转矩阵）得到，而这个变换矩阵本身，只依赖于相对距离 k，而与绝对位置 pos无关！，这个公式的本质上就是把以PE_{(pos)}为基础顺时针旋转k度。

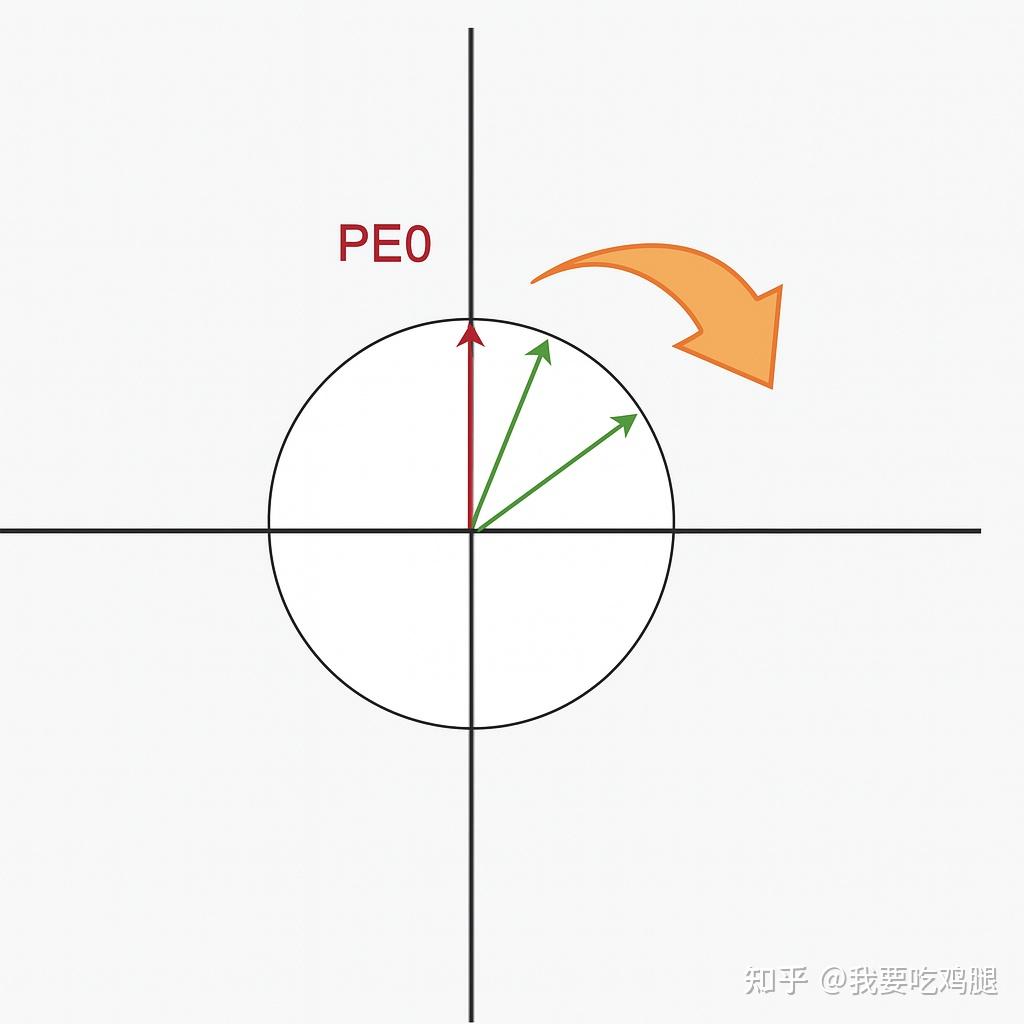
由于 \theta 是预先设定好的一个常数，所以当我们假设某个 t 固定不变，然后慢慢增大 k 时， \cos(k\omega_i) 逐渐变小，这也意味着相距较远的两个位置编码的内积越小，即内积可以用于反映两个位置向量在绝对位置上的远近

但是，细心的你一定发现了，如果我保持红色 PE_0 不变，顺时针慢慢转动绿色 PE 时，可能会出现下图的情况，即图中所示的两个绿向量和红向量的内积是一样的，但是左侧绿向量明显距离红向量更远。此时，我们似乎无法从内积大小判断两个位置向量的远近：

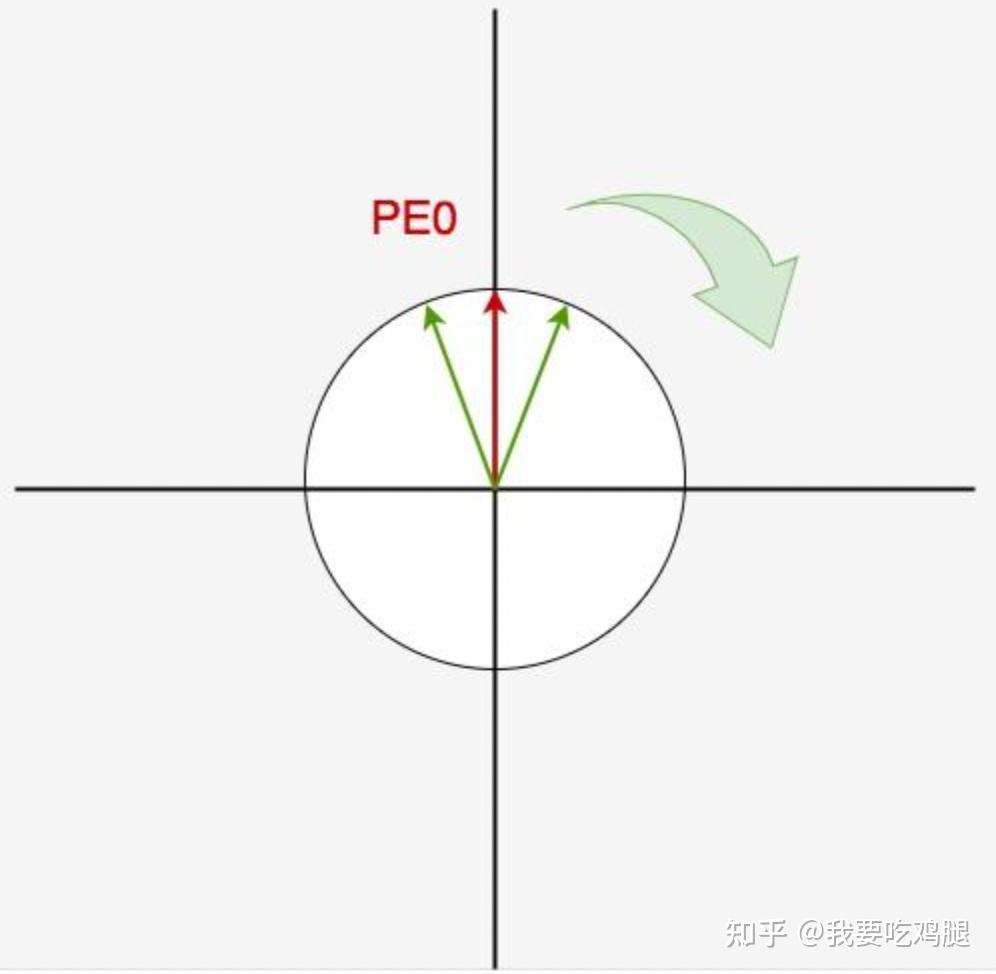
那该怎么办呢？我们有一个粗暴但有效的解决方法：让每次位置变动时的转动角度小一些，不就可以了吗？ 由于我们转动角度为 k\omega_i，这意味着只要我们尽量把 \omega_i 设置得小一些（这就意味着调大了 \cos(k\omega_i) 的周期），让绿线旋转的幅度小一些，使得不管有多少个位置信息，绿线都在第一和第四象限内移动，不就可以了吗？

在设置合适的 \omega_i 值的前提下，每个位置都能取到唯一的位置编码（绝对性）
一个位置编码可以由另一个位置编码旋转而来（相对性）
在设置合适的 \omega_i 值的前提下，两个位置编码的内积大小可以反应位置的远近，内积越小、距离越远（衰减性）。

具体我们可以看一下下面这张图，其中的横坐标是k也就是我们的位置，然后纵坐标是他们之间的点积，不同的颜色代表有不同的纬度大小。

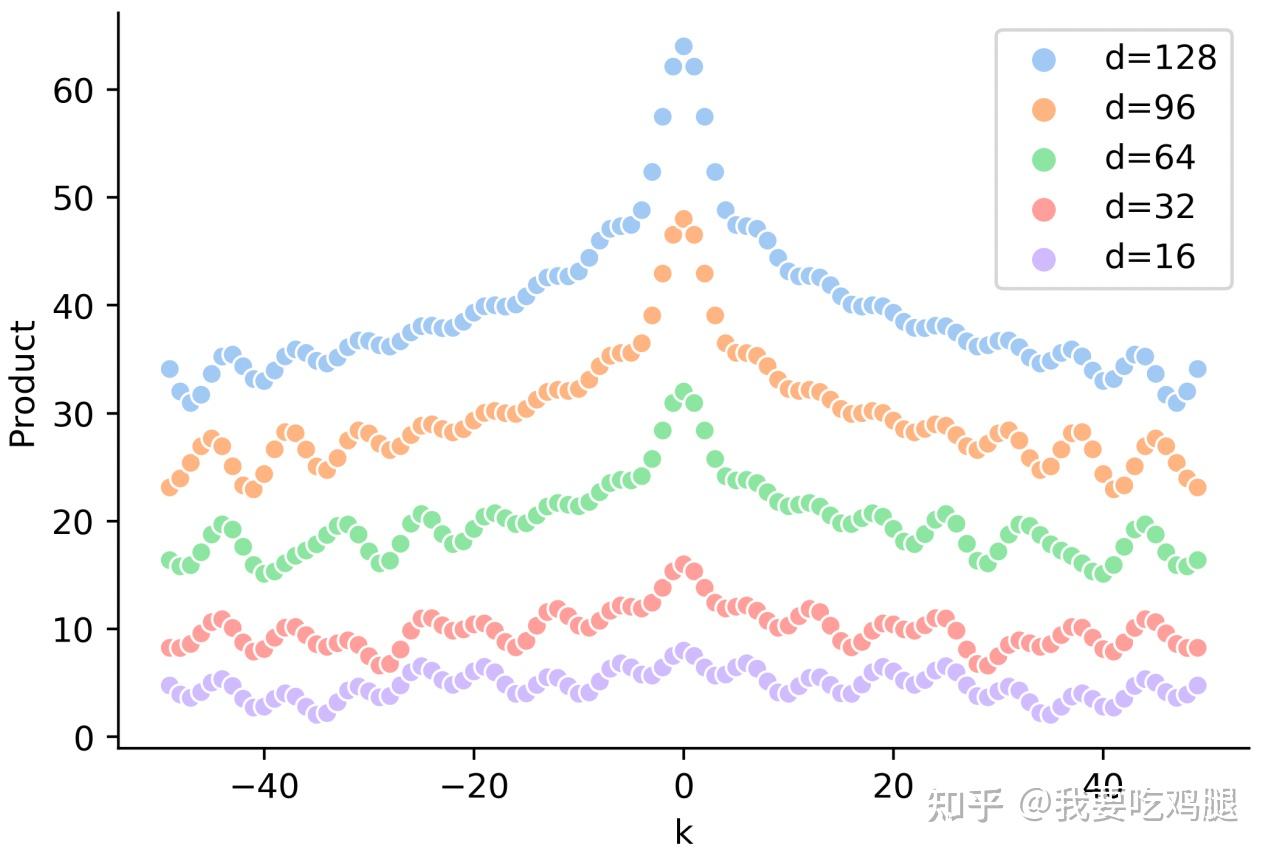
从图中我们可以发现：

在固定某个 PE_t 的情况下，两个位置编码的内积具有对称性（很简单，想象 \cos 函数的对称性。）
在固定某个 PE_t 的情况下，两个位置编码的内积具有远程衰减性（在上面实验图对应的原始论文中被称为**“距离意识（distance-aware）”**），即两个位置编码相距越远，内积越小。

这正是作者们声称其具备外推能力的理论基石。因为模型只要在训练中学会了如何处理这种由 k 决定的旋转变换，那么无论 pos有多大，它都应该能理解其相对位置关系。

现实中的“信息污染”

然而，理想很丰满，现实很骨感。尽管正弦编码在数学设计上如此优雅，但在实际的Transformer模型中，它的外推效果并不理想，性能依然会随着超出训练长度而下降。

其根本问题，出在了它与词向量的结合方式——加法，以及后续注意力层中复杂的非线性变换。

让我们一步步剖析这个理想是如何破碎的：

我们理想中那个只依赖于相对距离 k的、干净的线性变换关系，原本存在于PE_{pos}和PE_{pos'}之间。

但在经过了与词义信息（TokenEmbedding）的混合，以及被可学习的、对旋转特性一无所知的投影矩阵W_Q和W_K进行“蹂躏”之后，这个美好的关系在最终的点积计算中被彻底破坏了。模型最终看到的，是内容和位置信息相互纠缠、高度耦合的结果。

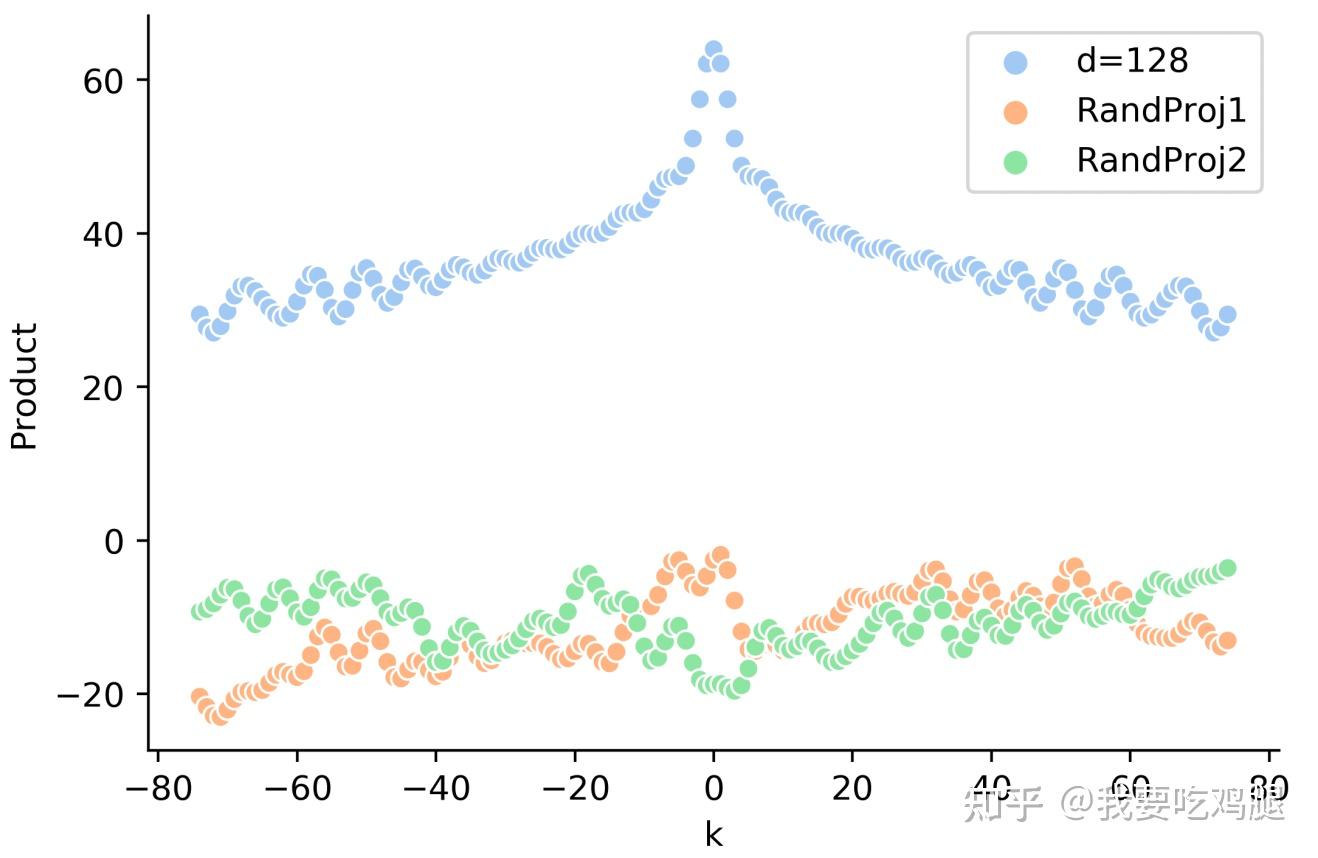
具体是怎么样影响的我们可以从这个实验里面看到，蓝色是纯位置关系，剩下两条是内容与位置耦合了之后算出来的点积，可以看到经过了这种耦合之后原始位置编码的优良性质（远程衰减性等）都受到了极大程度的破坏。

这种现象，被研究者们形象地称为 “信息污染”。注意力层的计算，非但没有利用好输入层位置编码的优良性质，反而将其摧毁了。最终，这种加性方案，终究未能完美地解决问题。

长久以来，学术界和工业界都在苦苦追寻一种能够同时满足以下条件的“圣杯”式位置编码方案：

具备相对性：能让模型自然地理解词与词之间的相对距离。
具备外推性：能轻松处理远超训练长度的文本。
无信息污染：能以一种更纯粹的方式融入模型，不干扰词义本身。
高效且无参：不增加额外的模型参数和计算负担。

正是对这些目标的不懈追求，最终引导我们走向了RoPE的革命性设计。

1.3 RoPE的登场：旋转吧，位置！

正是在这样的背景下，旋转位置编码（Rotary Position Embedding, RoPE） 如一道闪电划破长空，为上述所有难题提供了一个优雅得令人拍案叫绝的答案。它迅速被Llama、Qwen、ChatGLM等几乎所有现代顶级大语言模型所采纳，成为了事实上的行业标准。

RoPE的思路是颠覆性的。它彻底抛弃了“加法”的陈旧范式，转向了一种全新的、基于“乘法”的操作——或者更精确地说，是复数域的旋转。

它的核心思想可以这样理解：我们不再尝试给一个词向量“附加”一个位置向量，而是根据这个词的绝对位置，对它的 Query 和 Key 向量本身进行一次“旋转”。这种旋转操作，是通过乘以一个与位置相关的复数来实现的。

这个看似简单的操作，却带来了一个石破天惊般的结果：在后续注意力计算的点积环节，两个经过不同角度旋转的向量进行内积，其结果中，与绝对位置相关的信息被神奇地抵消了，最终只保留了与它们相对位置差值相关的信息！

如下图所示，RoPE在设计上的终极目标，就是让施加了绝对位置 m 和 n 的函数 f(q, m) 和 f(k, n)，在进行内积之后，其结果等价于一个只依赖于相对位置 m-n 的函数 g。这正是RoPE“通过绝对位置编码的方式实现相对位置编码”思想的精髓。

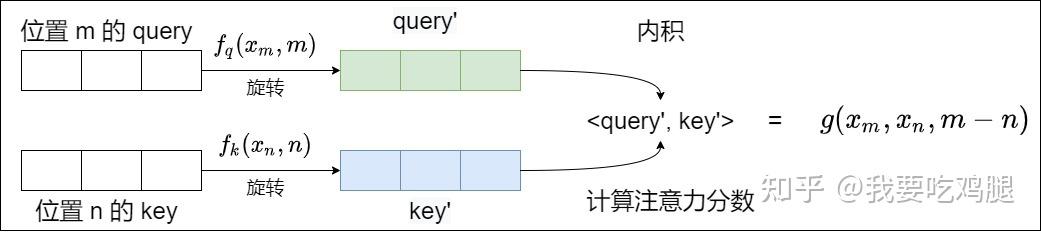
为了让这个“旋转”的概念更加直观，我们可以想象一下。同一个单词，比如“dog”，当它出现在句子的不同位置时（如第0位、第1位、第4位……），RoPE就会像一只无形的手，将这个词的向量相应地旋转一个与位置成正比的角度（比如0度、θ度、4θ度……）。

RoPE旋转示例

这种“四两拨千斤”的设计，几乎完美地满足了我们之前的所有期望。它不仅优雅地解决了相对位置的编码问题，还因为其连续的、基于三角函数的形式，天然具备了优秀的远程衰减特性和强大的长度外推潜力。

第二章、 RoPE的核心思想：用“旋转”赋予位置感

在上一章中，我们详细剖析了传统位置编码方案所面临的困境：可学习编码缺乏外推性，如同被无形的墙所禁锢；而设计精妙的正弦编码，其相对位置信息又在注意力层的复杂运算中被“污染”，理想最终未能照进现实。

这些问题共同指向了一个核心矛盾：我们如何在不破坏词义信息的前提下，将位置感“注入”到模型中，并让这种位置感能自然地体现为相对关系？

面对这一挑战，RoPE的提出者们进行了一次彻底的范式转移。他们不再纠结于如何设计一个与词向量相加的位置编码，而是提出了一个颠覆性的问题：我们能否不“添加”位置信息，而是直接“改变”词向量自身来蕴含位置？

这个“改变”并非随意扭曲，而是一种极其优雅、保留核心信息的变换——旋转。这便是RoPE思想的源点与核心。

2.1. 直观理解：从“叠加”到“旋转”的优雅一跃

让我们先构建一个直观的画面。传统的加性位置编码，好比我们有一个代表“苹果”这个词义的向量，为了告诉模型它在句子的第3个位置，我们又拿来一个代表“第3位”的位置向量，将两者直接相加。

这个过程虽然简单，但结果是一个全新的、混合了两种信息的“杂交”向量。我们很难再说清这个新向量里，哪部分是纯粹的词义，哪部分是纯粹的位置。

RoPE则提出了一种截然不同的、非破坏性的思路。它认为，一个词的核心语义信息，可以被看作是其向量的模长（或范数），而位置信息，则可以被编码为其向量的辐角（或方向）。

这个思想的转变是根本性的。它意味着，当我们想给一个词向量注入位置信息时，我们不应该改变它的模长（即不改变其核心语义），而仅仅需要改变它的方向——也就是对它进行一次旋转。

这种操作的优雅之处在于它的信息保真度。一次纯粹的旋转变换是保范的，它不会拉伸或压缩原始向量，从而完美地保留了向量所承载的全部语义信息。它只是在多维空间中，赋予了这个语义向量一个与位置相关的“姿态”或“朝向”。

为了让这个概念更加具体，让我们来看一个生动的例子。假设我们有一个向量代表单词 dog。

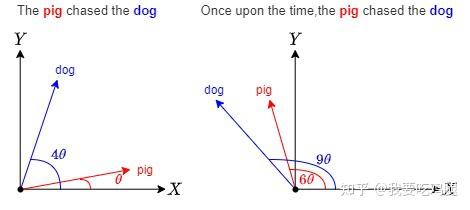
dog：单词dog在第0位，我们不对其进行任何操作，它的向量就指向原始方向。
The dog：当 dog出现在第1个位置时，我们将其向量逆时针旋转一个角度 \theta。
The pig chased the dog：当 dog出现在第4个位置时，我们将其向量逆时针旋转 4\theta。
Once upon the time, the ping chased the dong：当 dog出现在第9个位置时，我们将其向量逆时针旋转 9\theta。
以此类推，当它出现在第 m 个位置时，我们就将其旋转 m\theta 度。

如下图所示，同一个单词 dog，其核心语义（向量的模长）始终不变，但它在不同位置上的“表示”却因旋转角度的不同而独一无二。

RoPE旋转示例

这个简单的“旋转”操作，相比“叠加”，至少带来了两个显而易见的好处：

信息无损：语义信息和位置信息被解耦到了向量的模长和辐角上，相互独立，互不干扰。这彻底避免了加性方法中的“信息污染”问题。
天然的连续性和外推性：旋转角度 m\theta 是一个连续的量，这为模型理解位置的连续变化、并外推到未曾见过的更长位置 L\theta（其中 L > 训练长度）提供了可能。

这种将位置信息编码为旋转角度的直观思想，构成了RoPE整个理论体系的出发点。

2.2. 核心目标：定义位置编码的“终极形态”

有了直观的旋转思想后，我们需要将其转化为一个严谨的数学目标。RoPE的设计者们提出了一个极其深刻而精确的问题：我们能否设计一个函数 f，它能对 Query 和 Key 向量进行处理，使得经过处理后的两个向量在进行注意力核心运算——点积（内积）之后，其结果能够自动地、只体现出它们之间的相对位置关系？

这个问题可以被形式化为寻找一个函数 f(x, p)，其中 x 是原始向量（如 q 或 k），p 是其绝对位置，使得以下等式恒成立： \langle f(q, m), f(k, n) \rangle = g(q, k, m-n)让我们来仔细剖析这个堪称RoPE“设计总纲”的目标公式：

f(q, m) 和 f(k, n)：这是我们待求解的核心函数。它接收一个原始的、不含位置信息的向量（例如由第 m 个词元生成的 Query 向量 q），以及该词元所在的绝对位置 m。函数的输出，是一个全新的、已经蕴含了位置信息的 Query 向量。对 Key 向量 k 的处理同理。
\langle \cdot, \cdot \rangle：这个符号代表向量的**内积（点积）**运算。这至关重要，因为 q 和 k 的点积正是注意力分数计算的核心。这意味着我们的设计必须在注意力机制的根本运算上生效。
g(q, k, m-n)：这是我们期望达到的效果。公式的右侧是一个全新的函数 g，它的输入参数只有三个：原始的 q 向量、原始的 k 向量，以及它们的相对位置 m-n。

这个目标公式的深刻之处在于，它清晰地描述了一种“通过绝对，实现相对”的哲学。

我们在实现侧（公式左边），是对每个向量依据其绝对位置 m 和 n 进行独立操作的。但在效果侧（公式右边），我们希望得到的结果，却完全抹去了绝对位置的痕迹，只留下了它们之间的相对关系。

下图完美地诠释了这个核心目标：

这张图告诉我们，RoPE的实现方式（f函数）就像一个黑盒，我们将携带绝对位置 m和 n的 q和 k向量放进去，经过黑盒处理和内积运算后，我们惊奇地发现，输出的结果只与 q、k和它们的相对距离 m-n有关。

为什么实现这个目标如此重要？因为它直击了Transformer长度泛化的痛点。如果模型在计算注意力时，真的只依赖于相对距离（例如，“向前看1个词”、“向后看5个词”），那么它在训练时学会的这种相对关系，就应该能无缝地应用到任何绝对位置上。

无论是在句首、句中还是在一个前所未见的超长文本的末尾，模型处理“向前看1个词”的机制都应该是一致的。这正是实现真正长度外推的关键所在。

2.3. 几何之美：为何“旋转”是实现目标的完美工具？

既然我们已经明确了目标，下一步就是寻找一个具体的数学工具来实现这个神奇的 f 函数。“旋转”这个直观的念头，在严谨的数学审视下，被证明是实现该目标的不二之选。其完美性体现在旋转矩阵（Rotation Matrix）所具备的几个关键数学性质上。

为简单起见，我们先从二维空间开始。在二维平面上，将一个向量 (x, y) 逆时针旋转 \theta 角，等价于左乘一个旋转矩阵

R_\theta

：

R_\theta = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}

这个简单的旋转操作，恰好拥有我们梦寐以求的特性：

特性一：正交性（Orthogonality）

旋转矩阵是正交矩阵，满足 R_\theta^T R_\theta = I，其中 R_\theta^T 是其转置。这意味着旋转变换保持向量的模长不变。

\|R_\theta \mathbf{v}\|^2 = (R_\theta \mathbf{v})^T (R_\theta \mathbf{v}) = \mathbf{v}^T R_\theta^T R_\theta \mathbf{v} = \mathbf{v}^T I \mathbf{v} = \mathbf{v}^T \mathbf{v} = \|\mathbf{v}\|^2

这个性质至关重要。如前所述，q 和 k 向量的模长可以被认为是其核心语义强度的体现。旋转操作只改变方向，不改变大小，确保了我们在注入位置信息的同时，没有以任何方式“污染”或“扭曲”原始的语义信息。这正是对加性方案“信息污染”问题的完美回应。同时，保持模长也有助于训练过程的数值稳定性。

特性二：群论性质 (Group Property)

旋转矩阵构成了一个特殊的群（二维特殊正交群 SO(2)），这个群的运算性质，正是实现“绝对转相对”戏法的关键。具体来说：

旋转的叠加性：连续进行两次旋转，等价于一次性旋转两个角度之和。
R_{\theta_1} R_{\theta_2} = R_{\theta_1 + \theta_2}
转置与逆旋转：一个旋转矩阵的转置，恰好等于它的逆矩阵，也等于一个反向旋转。
R_\theta^T = R_\theta^{-1} = R_{-\theta}

让我们停下来，仔细品味这个最终结果。等式的左边，是我们对处于绝对位置 m 和 n 的向量进行操作和计算。而在等式的右边，最终的内积值，取决于三个因素：原始的 q 向量、原始的 k 向量，以及一个旋转矩阵 R_{(n-m)\theta}。而这个旋转矩阵，它的旋转角度只依赖于相对距离 n-m！

绝对位置 m 和 n 本身，已经在数学推导的火焰中被熔炼、抵消，最终只留下了它们之间相对关系的结晶。这完美地、毫无瑕疵地实现了我们最初设定的宏伟目标。

至此，RoPE的核心思想已经完整展现。它通过一次优雅的范式转移，从“叠加”走向“旋转”，并巧妙地利用了旋转操作的几何与代数性质，找到了一条无需学习参数、不污染语义信息、又能将绝对位置编码自然转化为相对位置感知的康庄大道。

第三章、精密时计：从二维到高维的实现

在上一章中，我们已经领略了RoPE“通过旋转注入位置信息”的核心思想，并通过旋转矩阵的性质，在概念上验证了这一思路的可行性。现在，是时候揭开 f 函数内部的神秘面纱了。

我们将从最简单的二维情况入手，借助复数的强大威力，一步步推导出RoPE的具体实现，并最终将其扩展到适用于真实模型的高维向量空间。

3.1 数学工具的准备：拥抱复数与欧拉公式

为了将“旋转”这一几何概念转化为可计算的代数形式，我们引入两个强大的数学工具：复数（Complex Numbers） 和 欧拉公式（Euler's Formula）。

不了解的朋友可以先看这一篇文章：深入浅出复数与欧拉公式：如何用“旋转”思想理解波与振荡？（非常好懂，有高中知识即可）

3.1.1 从二维向量到复数

任何一个二维实数向量 \mathbf{v} = (v_1, v_2) 都可以被唯一地表示为一个复数 z = v_1 + i v_2，其中 i 是虚数单位，满足 i^2 = -1。这个简单的映射，为我们打开了一扇通往全新计算维度的大门，并且我们的坐标是可以用极坐标来表示的，即用角度+长度来表示，这样就可以把位置信息和语义信息分离开。

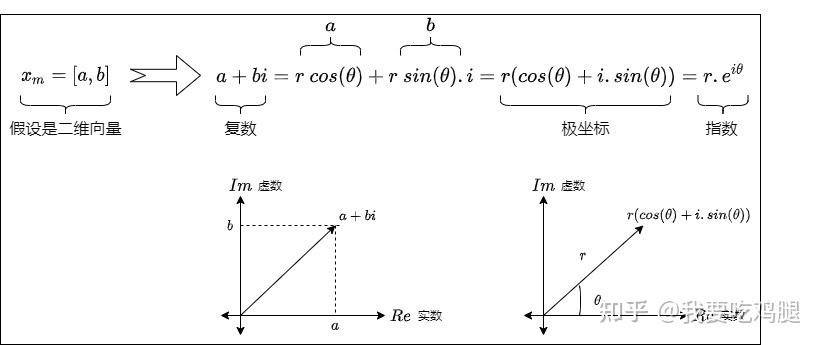
在复平面上，复数 z 就对应着从原点指向点 (v_1, v_2) 的向量。这种对应关系的美妙之处在于，复数的乘法运算在几何上恰好对应着向量的旋转和缩放。

具体来说，如果我们将两个复数相乘，z_1 = r_1(\cos\theta_1 + i\sin\theta_1) 和 z_2 = r_2(\cos\theta_2 + i\sin\theta_2)，其结果为：

z_1 z_2 = r_1 r_2 (\cos(\theta_1+\theta_2) + i\sin(\theta_1+\theta_2))

几何意义是：模长相乘，辐角相加。

这个性质对我们来说极其重要。如果我们想对一个向量进行一次纯粹的旋转（不改变模长），我们只需要让它乘以一个模长为1的复数即可。

3.1.2 欧拉公式：连接指数与三角的桥梁

哪个复数的模长恰好为1呢？欧拉公式给出了最优雅的答案： e^{i\theta} = \cos\theta + i\sin\theta这个公式告诉我们，任何一个虚数指数 e^{i\theta}，都对应着复平面单位圆上一个辐角为 \theta 的点。它的模长永远是 \sqrt{\cos^2\theta + \sin^2\theta} = 1。

因此，将一个代表向量的复数 z 乘以 e^{i\theta}，其几何效果就是将该向量逆时针旋转 \theta 角，而保持其模长不变。 z \cdot e^{i\theta} \implies \text{将向量 } z \text{ 旋转 } \theta \text{ 角}

这正是我们实现RoPE所需要的、最完美的数学工具。它将复杂的二维旋转矩阵运算，简化成了一次优雅的复数乘法。

3.1.3 定义二维空间下的 f 函数

有了复数和欧拉公式的加持，我们现在可以正式地、精确地定义在二维空间中，RoPE是如何对 Query 和 Key 向量进行操作的。

假设我们的 Query 向量 q 和 Key 向量 k 都是二维的，即 q=(q_0, q_1) 和 k=(k_0, k_1)。

向量复数化：首先，我们将这两个二维向量解释为复数：

q_{\mathbb{C}} = q_0 + iq_1 \quad \text{和} \quad k_{\mathbb{C}} = k_0 + ik_1

定义旋转操作：根据上一章的核心思想，我们要对处于位置 m 的 q 向量旋转 m\theta 角，对处于位置 n 的 k 向量旋转 n\theta 角。利用欧拉公式，这个旋转操作可以表示为乘以一个模长为1的复数：

对 q 的旋转因子：e^{im\theta}
对 k 的旋转因子：e^{in\theta}

这里的 \theta 是一个预先设定的、与维度相关的常数（我们稍后会讨论它的取值），它决定了旋转的基础“速率”。

正式定义 f 函数：现在，我们可以写出 f(x, p) 的具体形式了。它将原始的 Query向量（此时已是复数形式）乘以对应的旋转因子：

f(q, m) \triangleq q_{\mathbb{C}} \cdot e^{im\theta} = (q_0 + iq_1) e^{im\theta}

同样地，对于 Key向量：

f(k, n) \triangleq k_{\mathbb{C}} \cdot e^{in\theta} = (k_0 + ik_1) e^{in\theta}

至此，我们已经用复数乘法精确定义了 f 函数。它接收一个二维向量（q或 k）和一个绝对位置（m或 n），输出一个经过旋转的、代表新状态的复数，梳理一下流程大概长这样：

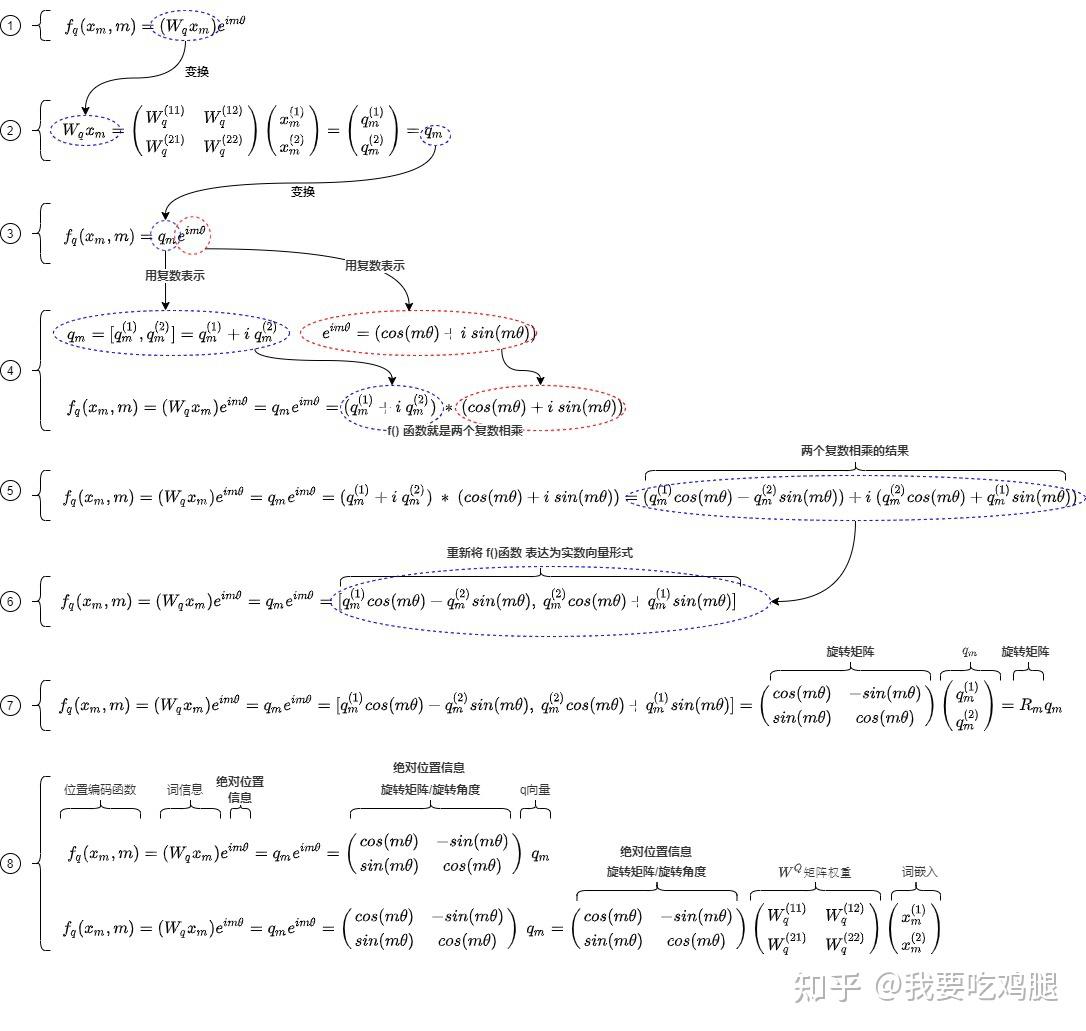
3.1.4 验证：在复数域中实现“绝对转相对”

现在，最关键的一步来了：我们需要验证我们定义的这个 f 函数，在经过内积运算后，是否真的能够涌现出我们所期望的、只依赖于相对位置 m-n 的特性。

然而，我们面临一个小问题：内积是定义在实数向量空间的操作，而我们的 f 函数输出的是复数。我们如何计算两个复数之间的“内积”呢？

让我们来解读这个最终的、至关重要的结果。这个表达式告诉我们，经过RoPE处理后的 q和 k的内积，等价于两部分复数乘积的实部：

q_{\mathbb{C}}^* \cdot k_{\mathbb{C}}：这一部分只与原始的、未经旋转的 q和 k向量有关。它代表了纯粹的内容相似度。
e^{i(n-m)\theta}：这是一个旋转因子，而它的旋转角度，不多不少，正好是相对位置 n-m 乘以基础速率 \theta。

绝对位置 m 和 n 再一次、也是最终一次，在数学的熔炉中被提炼，只留下了它们的相对差值。这证明了，我们基于复数旋转所构建的 f 函数，完美地实现了RoPE的核心设计目标。

下图直观地展示了这个过程：q和 k向量首先被各自的绝对位置旋转，但在计算内积时，这个过程等价于先计算原始向量的“内容关联”，再将这个关联结果根据它们的相对位置进行一次旋转。

3.1.5 回到实数域：最终的实现形式

尽管复数域的推导过程无比优雅，但在实际的深度学习框架（如PyTorch或TensorFlow）中，我们操作的都是实数张量。因此，最后一步，我们需要将复数域的旋转操作，翻译回等价的实数域矩阵运算。

我们回顾一下 f 函数的定义：f(q, m) = (q_0 + iq_1) e^{im\theta}。

我们发现，这个 2 \times 2 的矩阵，正是我们在第二章中作为直观理解所引入的旋转矩阵 R_{m\theta}！

这表明，f 函数在实数域中的具体实现，就是对原始的二维向量 q 左乘一个与位置 m 相关的旋转矩阵。这不仅在数学上完成了闭环，也为我们在高维空间中的实现指明了方向。

至此，我们已经完整地、详尽地剖析了RoPE在二维空间中的数学原理。我们从复数和欧拉公式出发，定义了旋转操作，并在复数域中严谨地证明了它可以实现“绝对转相对”的目标，最后又将其无损地翻译回了我们熟悉的、可在代码中实现的实数矩阵运算。

这个过程充分展现了RoPE设计的严密性与数学之美。接下来，我们将以此为基础，探讨如何将这一思想扩展到真实模型中数百甚至数千维的高维向量上。

3.2 时针与秒针：高维空间的多频旋转

我们在上一节中，已经彻底搞清了RoPE如何在二维空间中，通过复数乘法（等价于旋转矩阵）这一优雅的操作，将绝对位置信息无损地编码为向量的旋转，并在内积中自然涌现出相对位置关系。

然而，真实的大型语言模型，其内部处理的 Query和 Key向量并非简单的二维向量，它们的维度（d_{\text{model}}）通常是数百甚至数千维（例如128, 256, 4096等）。

这就给我们提出了一个严峻的挑战：我们该如何将一个二维平面上的旋转操作，推广到一个难以想象的、拥有成百上千个维度的高维空间中去呢？

一个天真的想法可能是去构造一个d \times d维的高维旋转矩阵。但这在数学上极其复杂，计算上更是灾难性的。更重要的是，一次性的高维旋转很难再保持我们在二维情况下所发现的那种清晰、简单的相对位置关系。

面对这个挑战，RoPE的作者们采取了一种极其聪明且高效的策略，可以概括为 “分而治之，各司其职”。

3.2.1 分而治之：将高维空间分解为二维子空间的集合

RoPE的核心思想，不是在整个高维空间中进行一次复杂的、统一的旋转，而是将这个庞大的 d维空间，巧妙地分解成 d/2 个相互独立、互不干扰的二维子空间。

具体来说，对于一个 d维的向量 \mathbf{v} = (v_0, v_1, v_2, v_3, \dots, v_{d-2}, v_{d-1})，我们将其相邻的维度两两配对，形成 d/2 个二维向量：

第0个子空间，由维度 (v_0, v_1) 构成。
第1个子空间，由维度 (v_2, v_3) 构成。
...
第 i个子空间，由维度 (v_{2i}, v_{2i+1}) 构成。
...
最后一个子空间，由维度 (v_{d-2}, v_{d-1}) 构成。

通过这种方式，一个复杂的高维向量操作问题，就被成功地转化为了 d/2 个我们已经完全掌握的、简单的二维向量旋转问题。我们只需要在每一个独立的二维子空间上，应用上一节推导出的旋转操作即可。由于内积运算满足线性可加性（即

\langle \mathbf{a}+\mathbf{b}, \mathbf{c} \rangle = \langle \mathbf{a}, \mathbf{c} \rangle + \langle \mathbf{b}, \mathbf{c} \rangle

），将所有子空间的结果相加，最终的内积结果依然能够保持我们所期望的相对位置特性。

3.2.2 时针与秒针：高维空间的多频旋转

如果我们将高维空间简单地分解后，让每一个二维子空间都以相同的角度 m\theta 旋转，那将是对高维表达能力的巨大浪费。这就像一块只有一根指针的时钟，虽然能转，但无法精确地表示复杂的时间。

为了打破这种单调性，RoPE在此借鉴了原版Transformer正弦位置编码的灵魂，并将其提升到了一个全新的高度：它没有为所有维度对（子空间）设定统一的旋转速率，而是为每一对都赋予了截然不同的基础旋转速率 \theta_i。

这个速率 \theta_i 的取值，遵循一个精心设计的、能够产生频率光谱的公式： \theta_i = \frac{1}{\text{base}^{2i/d_{\text{model}}}}通常情况下，超参数 base 取值为10000，d_{\text{model}} 是向量的总维度，而 i 则是二维子空间的索引（从0到 d_{\text{model}}/2 - 1）。

这个公式的引入，是RoPE的点睛之笔。它将一个高维向量，变成了一块由多个指针协同工作的精密时计。这个想法，与我们日常生活中最熟悉的钟表不谋而合。

一块钟表，正是通过不同频率的指针（时针、分针、秒针）的组合，来唯一地标识每一个“时刻”。RoPE的设计哲学与此如出一辙：

高频维度 (如同秒针)：当 i 很小（靠近0）时，\theta_i 很大（接近1）。这些维度对的旋转速度极快，如同钟表上的秒针。它们对位置的微小变化极其敏感，哪怕相对距离只移动1，其旋转角度也会发生剧烈变化。这使得模型能够精确捕捉局部的、细粒度的相对位置信息，例如区分“苹果手机”和“手机苹果”这两个词序紧邻的组合。
低频维度 (如同时针)：当 i 很大（靠近 d_{\text{model}}/2 - 1）时，\theta_i 变得非常小。这些维度对的旋转速度极为缓慢，如同钟表上的时针。它们的旋转角度在很长的距离内都保持相对稳定。这为模型提供了宏观的、粗粒度的坐标感，使其能够感知一个词元在整个长序列中的全局位置。

因此，一个词元在位置 m 的最终位置编码，就是由 d/2 个不同转速的指针共同指向的一个独一无二的“时刻”。如下图所示，从位置 m=0到 m=1，代表“秒针”的维度旋转幅度最大，而代表“时针”的维度则几乎不动。

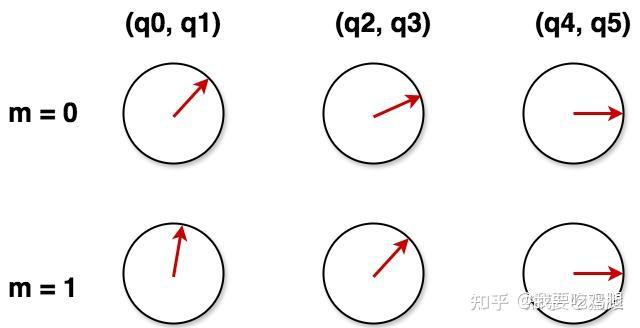
从傅立叶变换的视角看RoPE：这种用多种不同频率的周期函数来合成一个复杂信号的思想，并非凭空而来，它植根于一个深刻的数学原理——傅立叶分析。
傅立叶分析的核心思想是：任何复杂的信号（或函数），都可以被分解为一系列不同频率和振幅的简单正弦/余弦波的叠加。如下图的方波所示，通过不断叠加更高频率的蓝色正弦波，我们可以越来越精确地逼近原始的红色方波。

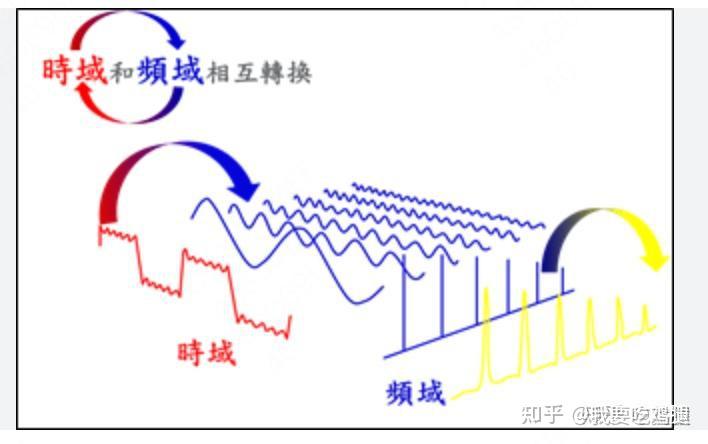
RoPE可以被看作是这一思想的逆向应用。它并非去分解一个已有信号，而是主动地为每一个位置 m，通过一组预设的、覆盖了从高到低频谱的旋转（即 cos和 sin波），构建出一个独一无二的、复合的“位置信号”。每一个二维子空间，就像是这个位置信号的一个傅立叶分量。

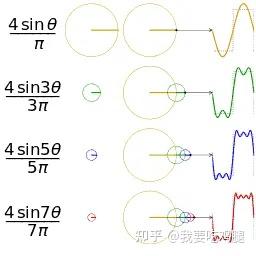
正是这种多频率的构造，赋予了RoPE同时感知“秒针”级的精细变化和“时针”级宏观结构的能力，使其在理解语言的复杂层次时游刃有余。

最终，对于一个 d维向量 q_m，我们将其相邻维度两两配对，每一对 (q_{2i}, q_{2i+1}) 都被视为一个独立的“指针”，并以其独特的速率 \theta_i 进行旋转。这 d/2 个指针共同协作，为 q_m 打上了精准而丰富的位置烙印。、

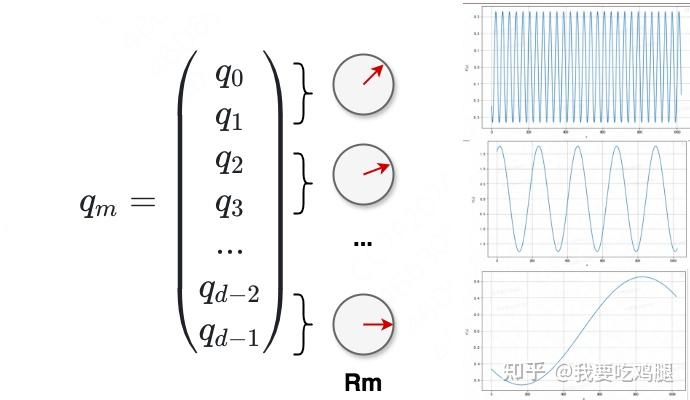
3.2.3 整体变换：一个优美的块对角旋转矩阵

从整体上看，对一个 d维向量施加RoPE，等价于左乘一个巨大的 d \times d 维的变换矩阵。由于每个二维子空间的旋转是相互独立的，这个巨大的变换矩阵呈现出一种非常优美且稀疏的结构——块对角矩阵（Block-Diagonal Matrix）。

这个矩阵的主对角线上，排列着 d/2 个 2 \times 2 的旋转矩阵块，而所有非对角块的元素都为0。对于位置为 m的向量，其变换矩阵 R_{m}^d 如下所示：

R_{m}^d = \begin{pmatrix} \cos(m\theta_0) & -\sin(m\theta_0) & \cdots & 0 & 0 \\ \sin(m\theta_0) & \cos(m\theta_0) & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & \cos(m\theta_{d/2-1}) & -\sin(m\theta_{d/2-1}) \\ 0 & 0 & \cdots & \sin(m\theta_{d/2-1}) & \cos(m\theta_{d/2-1}) \end{pmatrix}

于是，对一个高维向量 q 应用RoPE的完整过程，在数学上可以表示为： \tilde{q} = R_{m}^d \cdot q

这个矩阵的结构如下图所示，它清晰地揭示了RoPE“分而治之”的本质。

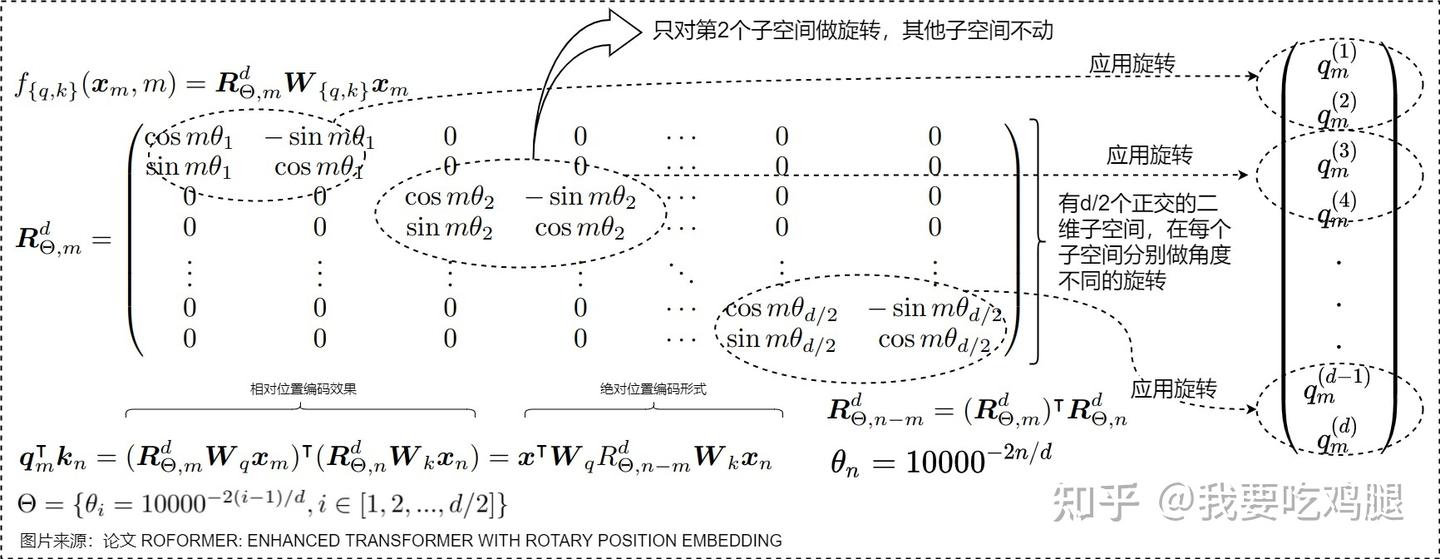
这个变换矩阵 R_{m}^d 同样是一个正交矩阵，因为它是由一堆正交的 2 \times 2 旋转矩阵拼成的。因此，它也完美地保持了高维向量的模长，不会对原始语义信息造成任何损失，并有助于整个模型的训练稳定性。

如下图所示，一个高维的 q向量在位置 m处，其内部的每一对维度都会根据自己独特的频率 \theta_i 进行旋转，共同构成最终的位置编码。

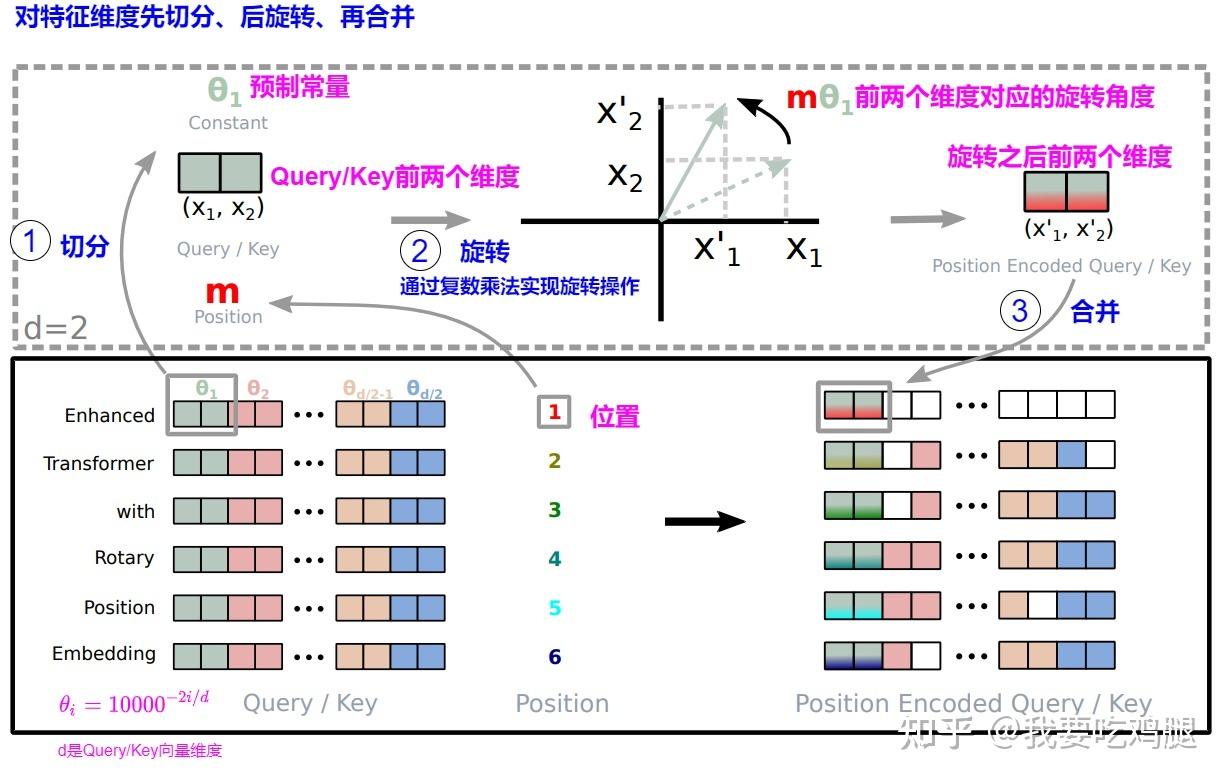
3.2.4 工程实现：告别矩阵乘法，拥抱元素级运算

虽然块对角矩阵在理论上很优美，但在实际的工程实现中，去构建并乘以一个如此巨大的稀疏矩阵是非常低效的。聪明的工程师们找到了一种更高效的、基于元素级（Element-wise）运算的实现方式。

这种方式的核心思想，是预先计算出所有位置、所有维度所需要的 cos 值和 sin 值，然后通过巧妙的向量操作来模拟旋转。具体步骤如下：

预计算 cos 和 sin 缓存：我们可以提前计算好一个形状为 [max_seq_len, d/2] 的 cos 缓存和 sin 缓存。
向量重塑与元素级乘法：将原始的 d维向量 q 分成两半，前 d/2维为 q_part1，后 d/2维为 q_part2。然后执行以下操作：

\tilde{q}_{part1} = q_{part1} \cdot \cos - q_{part2} \cdot \sin

\tilde{q}_{part2} = q_{part2} \cdot \cos + q_{part1} \cdot \sin

合并结果：将 \tilde{q}_{part1} 和 \tilde{q}_{part2} 拼接起来，就得到了最终旋转后的向量。

这个过程，在数学上与左乘块对角矩阵是完全等价的，但它将昂贵的矩阵乘法，转化为了硬件（如GPU）极其擅长的、可以高度并行化的元素级乘法和加法，极大地提升了计算效率。

下图以一种更通用的形式，直观地展示了这种高效的实现方式，其中 \otimes 代表元素级乘法（Hadamard Product）：

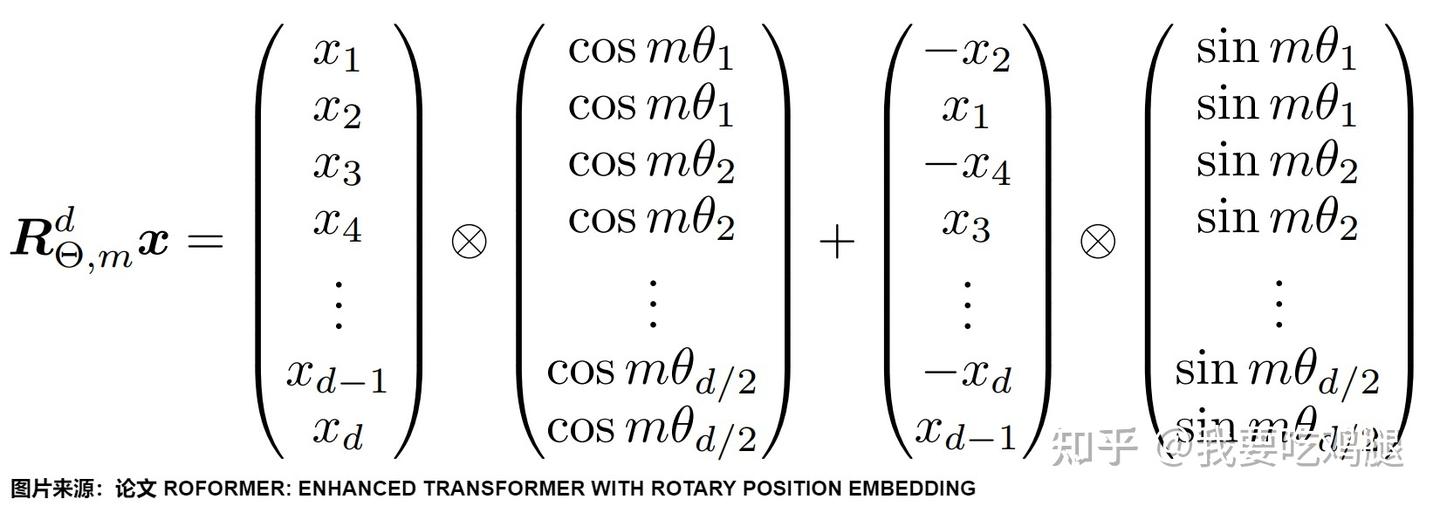
通过这种从理论到工程的精妙转化，RoPE不仅在数学上做到了自洽与优雅，在实际应用中也兼顾了极致的性能。

它就像一个精密的时钟系统，用不同速度旋转的指针（维度对），为序列中的每一个词元都打上了独一无二、又蕴含着丰富相对关系的时间烙印，为大语言模型的崛起奠定了坚实的基础。

3.3 关键推导总结：一个公式的最终胜利

经过前面两小节从二维复数域到高维块对角矩阵的逐步构建，我们已经将RoPE的实现细节一一剖析。这个过程充满了精巧的数学变换，现在，是时候退后一步，从全局的视角审视我们的推导成果了。

我们将把所有复杂的中间步骤，浓缩成一个最终的、能够体现RoPE全部智慧的核心公式，并以此来宣告这场数学推导的最终胜利。

3.3.1 回顾：我们构建了什么？

3.3.2 最终的核心恒等式

3.3.3 解读最终公式：三位一体的完美融合

让我们像解剖一件艺术品一样，仔细审视这个最终公式的每一个组成部分：

\underbrace{q^T}_{\text{内容1}} \quad \underbrace{R_{n-m}^d}_{\text{相对位置}} \quad \underbrace{k}_{\text{内容2}}

这个内积结果，完美地实现了内容与位置的动态融合，其计算过程可以被理解为三位一体的交互：

纯粹的内容关联 (q^T k)：如果没有中间的旋转矩阵 R_{n-m}^d（即当n-m=0时，R_0^d为单位矩阵I），这个公式就退化为标准的向量点积 q^T k。这代表了两个词元在语义层面的原始相似度，是注意力机制的基石。
相对位置的调制 (R_{n-m}^d)：这个旋转矩阵是RoPE的灵魂所在。它像一个精密的“调制器”，接收了 q和 k之间的相对位置差 n-m作为输入，然后对它们的内积结果进行一次复杂的、多维度的“调整”。

关键在于，这个调制器只关心“相对距离”，不关心“绝对坐标”。无论 q和 k是在句首（例如 m=1, n=3）还是在句末（例如 m=1001, n=1003），只要它们的相对距离 n-m都等于2，那么中间插入的旋转矩阵 R_2^d 就是完全相同的。
这个调整不是一个简单的标量惩罚（例如像其他相对位置编码方案那样，加上一个与距离相关的偏置项），而是一次真正的旋转变换。这意味着位置信息能以一种更丰富、更复杂的方式影响最终的注意力分数。

融合与输出：最终的注意力分数，是原始语义相似度在经历了相对位置的旋转调制后的结果。这使得注意力分数同时蕴含了两种信息：“这两个词在语义上有多相关？” 以及 “它们在序列中的相对位置关系是怎样的？”。

3.3.4 梦回起点：目标 g 函数的最终形态

现在，让我们回到第二章设定的那个宏伟目标：寻找一个函数 f，使得

\langle f(q, m), f(k, n) \rangle = g(q, k, m-n)

恒成立。

通过我们一路的推导，我们不仅找到了满足条件的 f函数（即乘以块对角旋转矩阵R_p^d），我们也自然而然地得到了目标函数 g的具体形态：

g(q, k, \Delta_{pos}) = q^T R_{\Delta_{pos}}^d k \quad \text{其中 } \Delta_{pos} = n-m

这个 g函数，就是RoPE为Transformer注意力机制带来的、内蕴了相对位置信息的全新“内积法则”。

下面的这张图，为我们整个复杂的推导过程提供了一个直观的视觉总结。它清晰地展示了，对两个经过RoPE旋转的向量求内积（公式左侧），其经过繁杂的三角函数展开与化简后，最终的结果与我们通过旋转矩阵性质推导出的简洁形式（公式右侧）是完全等价的。这张图，就是RoPE正确性的最佳视觉证明。

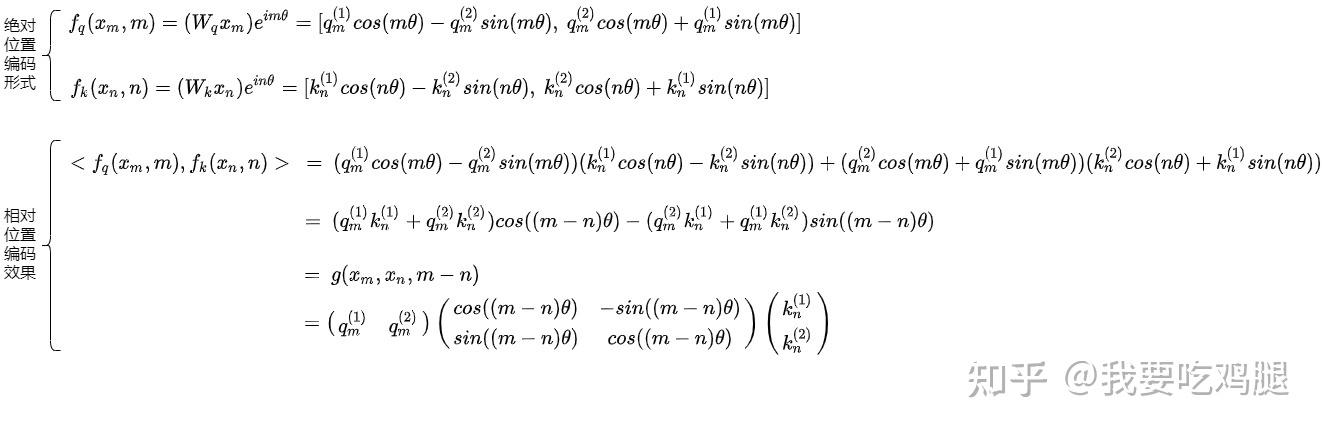
RoPE内积恒等式证明的可视化

综上所述，RoPE的数学推导之旅，是一场从直观的几何思想出发，借助复数、欧拉公式等优雅工具，最终构建出一个在代数上完美自洽、在工程上高效可行、并成功实现核心设计目标的典范。这个最终的核心恒等式——\langle f(q, m), f(k, n) \rangle = q^T R_{n-m}^d k是理解现代大语言模型位置编码技术的关键所在。

3.4 与正弦编码的对比：一场范式层面的革命

在深入剖析了RoPE的数学原理之后，我们有必要重新审视它的“精神前作”——原版Transformer提出的正弦位置编码（Sinusoidal Position Encoding）。从表面上看，两者都使用了三角函数（sin和cos），都采用了多频率的设计（通过10000^{2i/d}项），似乎颇有渊源。然而，如果我们深入其核心机制，就会发现两者之间存在的差异，并非简单的修补或改良，而是一场深刻的范式革命。

RoPE的胜利，在于它从根本上改变了位置信息与内容信息融合的方式以及作用的阶段。

3.4.1 融合方式的革命：从“线性叠加”到“旋转相乘”

这是两者最根本、最核心的区别，也是决定它们命运差异的关键所在。

正弦编码的“加法”世界：正弦编码遵循的是一种**线性叠加（Additive）的范式。它将预先计算好的位置向量 PE_{pos}，直接与词义向量 \text{TokenEmbedding} 相加，形成一个混合的输入向量： x_{\text{input}} = \text{TokenEmbedding} + PE_{pos}这种方式的本质，是将位置信息视为一种静态的、与内容无关的偏置（Bias）。它希望模型能够从这个混合体中，自主地学会分离和理解两种信息。然而，正如我们在之前章节中详细分析的那样，这个混合向量在经过后续注意力层中复杂的、可学习的线性投影（W_Q, W_K）后，原先精心设计的、基于三角函数和差角公式的相对位置关系，被严重地“污染”和破坏了。这种“先加后乘”的模式，导致了理想与现实的脱节。
RoPE的“乘法”世界： RoPE则开创了一种旋转相乘（Multiplicative）的范式。它并不在输入层对词向量做任何改动，而是将位置信息的作用阶段，后移到了 Query和 Key向量生成之后。更重要的是，它不是将位置信息“加”上去，而是将其作为一种旋转变换，“乘”上去： \tilde{q} = f(q, m) = R_m^d q这里的 q 是已经经过 W_Q 投影后、纯粹的“内容”向量。RoPE所做的，是对此内容向量进行一次保范的正交旋转。这种方式的本质，是将位置信息视为一种动态的、作用于内容向量的变换算子（Operator）。

下图直观地对比了这两种范式。正弦编码像是在原始向量上硬生生地“嫁接”了位置信息；而RoPE则是对向量进行了一次优雅的“旋转赋能”。

这场从“叠加”到“旋转”的革命，其意义远不止于形式上的改变。它从根本上解决了“信息污染”的问题，使得内容和位置两种信息能够在各自的轨道上保持纯粹，直到在最终的内积运算中才以一种高度结构化的、可控的方式进行交互。

3.4.2 作用阶段的革命：从“输入层注入”到“注意力层内交互”

融合方式的改变，自然也带来了作用阶段的后移，这同样是RoPE成功的关键。

正弦编码：正弦编码是一种前置（Upstream）处理方案。它在整个Transformer模型的最开端——输入层——就把位置信息完全融入了。这意味着，这些混合了位置信息的向量，必须经历后续所有网络层的复杂非线性变换。尤其是注意力层中的 W_Q 和 W_K 投影矩阵，它们在训练中，其优化目标是最小化最终的预测损失，而完全不会“顾及”到要保持输入向量中精巧的三角函数关系。因此，这种前置注入的方式，为后续的“信息污染”埋下了伏笔。
RoPE：RoPE则是一种精准介入（In-place Intervention）的方案。它选择在注意力机制内部、在 Query和 Key向量已经生成、即将进行点积运算前的最后一刻才“出手”。这个时机的选择堪称完美：

避免了W_Q, W_K的污染：q和 k向量在被旋转之前，是纯粹的内容表示，它们可以自由地通过W_Q, W_K进行语义空间的投影，而不用担心破坏任何位置结构。
直接作用于内积：RoPE的旋转操作，其目的就是为了直接影响和构建 q和 k的内积形式。将它放在内积运算之前，是最直接、最高效的方式，没有任何多余的中间环节可以干扰它的效果。

苏神（RoPE的提出者）曾精辟地指出，正弦编码失效的很大一部分原因，可能就是因为在投影矩阵 W_Q, W_K 之前进行了位置注入。而RoPE通过将旋转操作放在投影之后，巧妙地规避了这个问题，这或许正是它能够成功的关键所在。

3.4.3 能力边界的革命：从“有损表达”到“无损激发”

最后，两者在能力边界和潜力上也存在本质差异。

正弦编码：自身具备，但表达有损 正弦编码向量本身，通过其数学构造，是蕴含了相对位置信息的。理论上，模型可以学会从 PE_{pos} 和 PE_{pos+k} 的差异中解码出相对距离 k。然而，这种能力在与内容向量相加，并经过后续网络层处理后，其表达能力被大大削弱了，是一种**有损的（Lossy）**表达。
RoPE：自身不备，但内积激发 有趣的是，一个经过RoPE旋转后的向量 \tilde{q} = R_m^d q 本身，如果单独拿出来看，我们很难说它“蕴含”了什么清晰的相对位置信息。它的神奇之处，在于它是一种**“遇强则强”的编码。它的相对位置能力，是在与另一个同样经过RoPE编码的向量进行内积这个“仪式”中，才被激发（Elicited）出来的。 \langle \tilde{q}, \tilde{k} \rangle \implies \text{相对位置信息在此刻涌现}这是一种更高维度的设计：RoPE编码的不是一个静态的位置属性，而是一种动态的、与其它向量交互的潜能。

3.4.4 最终形态的革命：从“位置污染”到“结构化偏置”

在前面三个层面的对比中，我们已经从设计哲学、作用时机和能力展现方式上，深刻理解了RoPE相较于传统正弦位置编码（Sinusoidal PE）的压倒性优势。然而，要真正触及这场革命的核心，我们还必须回答一个终极问题：RoPE的这些精巧设计，最终在Transformer的心脏——注意力矩阵（Attention Matrix）——上，究竟呈现出怎样一种数学形态？为何这种形态能够从根本上杜绝“位置污染”，并实现完美的相对位置感应？

为了回答这个问题，我们需要引入一个重要的参照物，一个在相对位置编码领域同样声名显赫的方案——ALiBi（Attention with Linear Biases）。通过将RoPE的最终效果与ALiBi进行类比，我们将惊奇地发现，RoPE以一种隐蔽而优雅的方式，殊途同归地抵达了相对位置编码的“理想国”。

参照物：ALiBi的“显式偏置”哲学

ALiBi的思路极其直观，甚至可以说有些“简单粗暴”。它完全抛弃了在词向量上做文章的想法，而是选择在注意力计算的最后阶段进行“干预”。其核心步骤如下：

纯粹的内容关联：首先，模型像一个没有位置概念的Transformer一样，正常地计算出Query向量 q和Key向量 k，并算出它们之间的点积，得到一个只包含语义相似度的“纯内容”注意力分数： \text{Score}_{\text{content}}(q_m, k_n) = q_m^T k_n
添加线性偏置：接下来，ALiBi会计算一个只与 q和 k的相对位置 m-n相关的偏置项（Bias），并将其直接加到上述的内容分数上。这个偏置项是一个负的标量，其大小与相对距离成正比： \text{Bias}(m, n) = \text{slope} \cdot |m-n|这里的 slope是一个预设的、与注意力头相关的负数。距离越远，这个负向的偏置就越大，从而实现“距离惩罚”的效果。
最终注意力分数：最终的注意力分数，是内容与位置偏置的简单线性相加： \text{Score}_{\text{final}}(m, n) = q_m^T k_n + \text{slope} \cdot |m-n|

ALiBi的哲学是一种“后期修正”或“显式注入”。它认为内容和位置是两个完全独立的维度，应该分开处理，最后直接相加即可。这种方法的巨大优势在于：它从物理上就杜绝了 q、k投影矩阵对位置信息的任何污染，因为位置信息根本不参与投影。同时，它直接在注意力矩阵上引入了与相对位置相关的结构，强制模型去感知相对距离。

托普利茨矩阵：相对位置编码的“理想形态”

ALiBi的成功，揭示了一个深刻的本质：一个理想的相对位置编码方案，其最终作用于注意力矩阵上时，应该形成一种特殊的数学结构——托普利茨矩阵（Toeplitz Matrix）。

托普利茨矩阵的定义是：矩阵中每一条自左上至右下的对角线上的元素都完全相等。如下图所示：

A = \begin{pmatrix} a & b & c & d \\ e & a & b & c \\ f & e & a & b \\ g & f & e & a \end{pmatrix}

在注意力矩阵的语境下，这意味着什么呢？注意力矩阵的第 m行、第 n列的元素，代表着位置 m的Query对位置 n的Key的注意力分数。如果这个矩阵是托普利茨矩阵，那就意味着这个分数的值，只取决于 m和 n的差值 m-n（即它们属于哪条对角线），而与 m和 n的具体值无关。例如，Score(2,1)、Score(3,2)、Score(4,3)的值都将相等（都等于 e），因为它们的相对距离 m-n都是1。

这正是相对位置编码的终极目标！ 它意味着注意力机制已经完全摆脱了绝对位置的束缚，实现了完美的平移不变性（Shift Invariance）。无论一段对话发生在一个长文档的开头还是结尾，只要其内部的相对词距不变，其注意力模式就应该完全一样。

ALiBi通过其简单直接的加性偏置，强制地在注意力矩阵上构建了这种托普利茨结构。现在，我们回到RoPE，一个关键的问题摆在了我们面前：RoPE，这个看似复杂得多的、通过旋转操作实现的方案，它的最终效果是否也达到了这种理想的托普利茨形态呢？

RoPE的惊人等价性：隐式的结构化偏置

让我们再次请出RoPE的核心恒等式，这一次，我们要以前所未有的深度来审视它：

\text{Score}_{\text{RoPE}}(m, n) = \langle R_m^d q, R_n^d k \rangle = q^T R_{n-m}^d k$这个公式的右侧$q^T R_{n-m}^d k

，看起来与ALiBi的q^T k + \text{Bias}在形式上大相径庭。然而，魔法就隐藏在这看似不同的形式背后。

让我们将这个公式进行一次概念上的“拆解”。q^T R_{n-m}^d k实际上是在计算向量 q和向量R_{n-m}^d k的点积。后者是将原始的 k向量，根据相对位置 n-m进行了一次复杂的旋转变换。

这意味着，RoPE的最终注意力分数，并不仅仅是像ALiBi那样，在原始内容关联的基础上，简单地“加上”一个惩罚项。它做的是一件更精妙、更动态的事情：它根据相对位置 n-m，对Key向量 k本身进行了“扭曲”和“重塑”，然后再与原始的Query向量 q进行交互。这个由R_{n-m}^d带来的“旋转调整”，其效果等价于一个极其复杂的、依赖于内容的动态偏置。

更重要的是，这个最终的得分q^T R_{n-m}^d k，它的计算结果只依赖于原始的 q、k以及它们的相对距离 n-m。绝对位置 m和 n已经在这个公式中被彻底消除。这意味着，RoPE所产生的注意力矩阵，与ALiBi一样，也天然地具备了我们梦寐以求的托普利茨结构！

RoPE和ALiBi，就像是两位武林高手，虽然修炼的武功招式（实现方法）截然不同——一个修炼的是刚猛直接的“降龙十八掌”（显式加偏置），一个修炼的是精妙内敛的“太极拳”（隐式旋转变换）——但他们最终都达到了“无招胜有招”的最高境界，即在注意力矩阵上实现了完美的相对位置感知。

RoPE的胜利，在于它以一种“隐式”的、与内容深度融合的方式，实现了ALiBi“显式”添加偏置所追求的同样结构。 它不像ALiBi那样，将内容和位置视为两个独立的、最后才相加的“模块”。在RoPE的世界里，位置信息像一个无形的力场，它不直接现身，而是通过改变场内物体（q和 k向量）的“姿态”（旋转），来动态地、隐式地调节它们之间的相互作用力（注意力分数）。

苏神（RoPE的提出者）一语道破天机：RoPE形式上是一种绝对位置编码（因为它操作的是每个词的绝对位置 m和 n），但实际上给Attention带来的是纯粹的相对位置信息。 这场从“位置污染”到“结构化偏置”的革命，其意义在于：

传统正弦PE：试图在输入端引入相对位置的“基因”，但这个基因在经过 W_Q, W_K这个“大熔炉”后，被彻底破坏，最终的注意力矩阵结构混乱，位置信息被严重污染。
RoPE：它绕过了W_Q,W_K这个熔炉，选择在投影之后，直接通过旋转操作，为最终的注意力矩阵“雕刻”出了一个清晰的、只依赖于相对距离的托普利茨结构。这是一种釜底抽薪式的胜利，它从问题的根源——注意力矩阵的最终形态——上解决了问题。

至此，我们终于将RoPE的成功，追溯到了它在数学本质上的最终胜利。它不仅仅是在哲学理念上更胜一筹，更是在最终的数学效果上，达到了相对位置编码的“理想国”。

3.4.5 总结：一场彻底的思维与结构升级

让我们用一个全面升级的表格，来为这场深刻的革命做一个最终的总结，它将涵盖我们从理念到形态的所有洞察：

对比维度	正弦位置编码 (Sinusoidal PE)	旋转位置编码 (RoPE)	革命性意义
核心范式	加性 (Additive)：向量 + 位置	乘性 (Multiplicative)：向量 x 旋转	思维升级：从静态的“数据偏置”，升级为动态的“变换算子”。
作用阶段	输入层 (Upstream)	注意力层 (In-place)	时机升级：从易被污染的“前置注入”，升级为直击核心的“精准介入”。
能力体现	自身蕴含，但表达有损	交互激发，效果无损	能力升级：从编码一个静态的“位置属性”，升级为编码一种动态的“交互潜能”。
注意力结构	信息污染，结构破坏	引入结构化偏置 (隐式ALiBi/Toeplitz结构)	形态升级：从混乱无序的“位置噪声”，升级为保证平移不变性的“理想数学形态”。

这场革命的历程，如同一部波澜壮阔的史诗：

正弦PE的悲剧：它像一位伟大的悲剧英雄，怀揣着“通过绝对位置表达相对位置”的崇高理想。它精心设计了一套基于三角函数和差角公式的“屠龙之术”。然而，它错误地选择在巨龙（Transformer）的入口处（输入层）就亮出所有底牌。结果，它的“屠龙宝刀”（精巧的数学关系）在经过巨龙消化道（W_Q, W_K投影）的残酷蹂躏后，变得面目全非，最终在巨龙的心脏（注意力矩阵）处，只留下了一片混乱的残骸。它的理想，最终未能照进现实。
RoPE的胜利：RoPE则像一位洞悉全局的智者。它深刻地理解到，直接与巨龙的消化系统对抗是徒劳的。它选择了一条更聪明的道路：它让内容向量 TokenEmbedding独自去闯过 W_Q, W_K的考验，自己则隐匿身形，在最后一刻，当纯粹的 q和 k向量即将在心脏处相遇时，它才如鬼魅般现身。它没有直接攻击，而是施展了一套精妙的“旋转之舞”，改变了 q和 k的“舞姿”。这场由RoPE指挥的、蕴含着相对位置法则的双人舞，其最终呈现出的“舞蹈效果”（注意力分数），自然而然地形成了优美而和谐的托普利茨韵律。

可以说，RoPE继承了正弦编码利用三角函数和多频率思想的“灵魂”，但却为其量身定做了一副全新的、能够完美发挥其威力的“躯体”。它不再试图将位置信息强行“塞入”内容，而是让位置成为一种指挥内容向量在多维空间中“翩翩起舞”的指令。而最终的注意力分数，就是这场由内容和相对位置共同编排的双人舞所呈现出的、蕴含着深刻数学结构之美的最终杰作。

正是这场从“叠加”到“旋转”，从“污染”到“结构”的深刻革命，为现代大型语言模型铺就了通往更长、更远未来的坚实道路，也为我们理解人工智能的内在机制，提供了一个闪耀着智慧光芒的绝佳范例。

参考文献

1.探秘Transformer系列之（17）--- RoPE
https://www.cnblogs.com/rossiXYZ/p/18787343
2.Base of RoPE Bounds Context Length Xin Men etc.
https://arxiv.org/pdf/2405.14591
3.LLM时代Transformer中的Positional Encoding
https://zhuanlan.zhihu.com/p/664214907
4.LLM（廿三）：LLM 中的长文本问题
https://www.zhihu.com/people/zi-qi-dong-lai-1
5.LLaMA中的旋转位置编码（RopE）实现解读https://zhuanlan.zhihu.com/p/684113260
6.Long LLM第二篇——why RoPE?https://zhuanlan.zhihu.com/p/694825487
7.ROUND AND ROUND WE GO! WHAT MAKES ROTARY POSITIONAL ENCODINGS USEFUL?https://arxiv.org/pdf/2410.06205
8.RedHerring
https://www.zhihu.com/people/hu-zi-xia-91
9.RoPE外推的缩放法则 —— 尝试外推RoPE至1M上下文https://zhuanlan.zhihu.com/p/660073229
10.RoPE旋转位置编码深度解析：理论推导、代码实现、长度外推https://zhuanlan.zhihu.com/p/645263524
11.Transformer位置编码（基础）https://www.zhihu.com/people/liuxiaoran-34
12.Transformer位置编码（改进）https://www.zhihu.com/people/liuxiaoran-34
13.Transformer升级之路：10、RoPE是一种β进制编码https://spaces.ac.cn/archives/9675
14.Transformer升级之路：15、Key归一化助力长度外推https://spaces.ac.cn/archives/9859
15.Transformer升级之路：16、“复盘”长度外推技术https://spaces.ac.cn/archives/9948
16.Transformer升级之路：2、博采众长的旋转式位置编码https://spaces.ac.cn/archives/9948
17.Transformer改进之相对位置编码(RPE)
]https://zhuanlan.zhihu.com/p/105001610
18.https://arxiv.org/pdf/2104.09864.pdf
19.llama源代码逐行分析https://zhuanlan.zhihu.com/p/679819602
20.qwen源码解读3-解读QWenAttention模型的调用https://www.zhihu.com/people/xiaoguzai
21.transformers 库提供的 llama rope 实现https://github.com/huggingface/transformers/blob/main/src/transformers/models/llama/modeling_llama.py#L204
22.中文语言模型研究：(1) 乘性位置编码https://www.zhihu.com/people/bopengbopeng
23.位置编码算法背景知识https://www.armcvai.cn/2024-10-22/pe-basic.html
24.千问Qwen2 beta/1.5模型代码逐行分析(一)
https://zhuanlan.zhihu.com/p/695112177
25.浅谈LLM的长度外推https://zhuanlan.zhihu.com/p/645770522
26.深入剖析大模型原理 — Qwen Bloghttps://zhuanlan.zhihu.com/p/698212162
27.羡鱼智能：【OpenLLM 009】大模型基础组件之位置编码-万字长文全面解读LLM中的位置编码与长度外推性（上）https://zhuanlan.zhihu.com/p/626828066
28.羡鱼智能：【OpenLLM 010】大模型基础组件之位置编码-万字长文全面解读LLM中的位置编码与长度外推性（ 中）https://zhuanlan.zhihu.com/p/629015933
29.让研究人员绞尽脑汁的Transformer位置编码 - 科学空间|Scientific Spaceshttps://kexue.fm/archives/8130
30.LLM：旋转位置编码（RoPE）的通俗理解https://zhuanlan.zhihu.com/p/690610231
31.Effective Long-Context Scaling of Foundation Models
https://arxiv.org/pdf/2309.16039
32.HoPE: A Novel Positional Encoding Without Long-Term Decay for Enhanced Context Awareness and Extrapolation
https://arxiv.org/pdf/2410.21216